División de un segmento en una razón dada

Dividir un segmento dirigido en una razón dada significa segmentarlo en partes de forma tal que se encuentren las coordenadas de un punto  que satisface la comparación entre dos magnitudes.

En general, si la razón es de la forma , implica que el segmento se divide en a + b partes. Por ejemplo, si , el segmento se divide en 11 partes iguales.

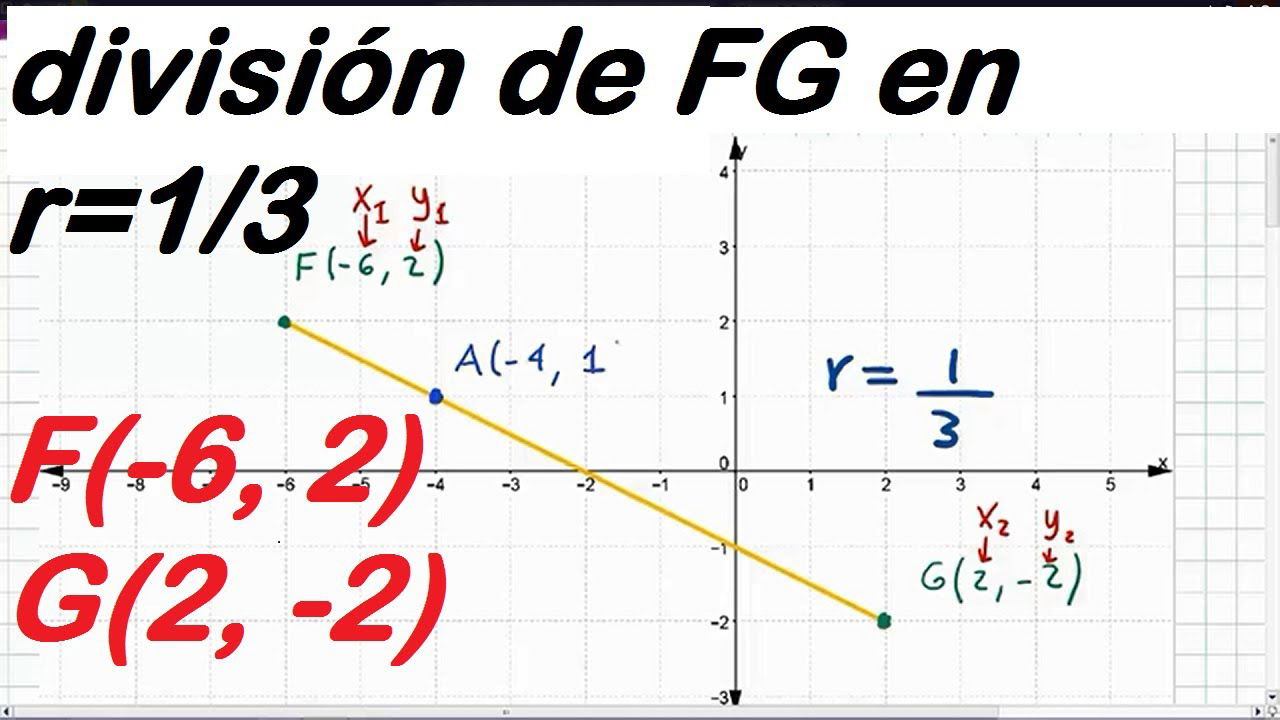
Sean los puntos,  así como el segmento de recta que los une:

Sea un punto  que pertenezca al segmento. Si se forman los triángulos mostrados, se observa que son semejantes. Esto es:

  y   

Donde r es la razón de proporcionalidad de semejanza.

Expresiones que sirven para obtener las coordenadas de un punto que divide a un segmento en una razón dada.

En el caso particular en que se trate del punto medio, r vale  , y las ecuaciones se convierten en:

   y   

CONCLUSIÓN

Con r = 0, el punto se ubica en  A medida que r va creciendo se desplaza hacia . En su punto medio r vale 1. Cuando r es negativa, el punto se ubica en su prolongación hacia abajo alejándose hasta que llega a r = -1 donde es infinito y cambia de sentido. Al seguir decreciendo, tiende a .